About our math solution
By math experts, for educational publishers
Learning is about growing, a continuous cycle of trying, reflecting, and improving. Educational technology carries great promise to enhance learning efficacy. However, developing such technology is a huge challenge.
We created tools that help students learn, and our mission is to bring these tools to you. Our product is a math API that adds intelligent math capabilities to your learning platform and generates data on your learner’s understanding and skills.
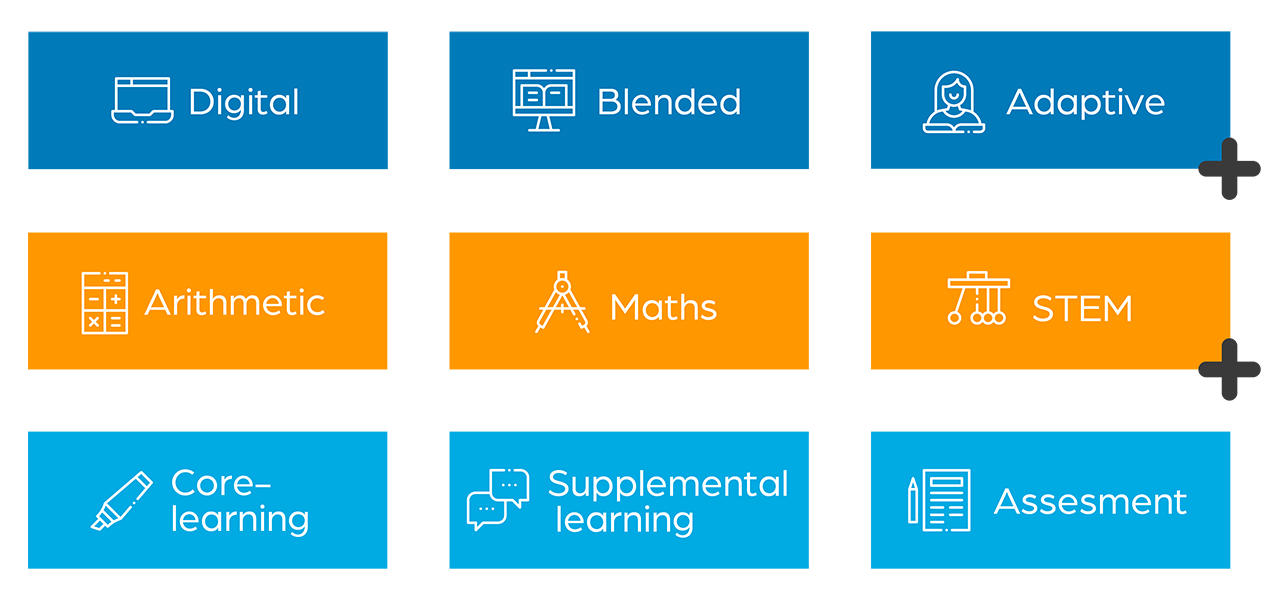
Use cases
Step 1. Your online strategy
You can use Algebrakit in blended, full-digital, and adaptive ways of teaching.
Step 2. Your subject
Our tools are designed for multi-step exercises in math, arithmetic and STEM.
Step 3. Your didactical approach
Algebrakit is suitable for core learning, supplemental learning and assessment.
Your online strategy
If you offer an online environment to complement your physical resources, you can use Algebrakit for unlimited practice questions and formative tests. Some clients let teachers create their own items and assign these to their students.
If you go fully digital with your digital learning environment, Algebrakit gives you the question types needed to cover the entire curriculum aligned to your local math standards.
The multi-step assessment features of Algebrakit generate a wealth of learning data to power your adaptive algorithms. For instance, we tag incorrect steps to identify misconceptions, enabling automatic detection of learning gaps.
Your subject
Although the name might suggest otherwise, Algebrakit supports much more than just algebra. Our tools suit all math subjects, such as equations, calculus, geometry, statistics, sequences, etc.
We also offer various tools for arithmetic in primary and secondary education, like multi-digit calculations, ratio tables, model methods (bar diagrams) and arithmetic word problems.
Algebrakit is also a powerful solution for STEM with its extensive support for units, accuracy, scientific formulas, and word problems.
Your didactical approach
Algebrakit is used by educational publishers for solutions offered in schools, edTech providers who create engaging student-facing apps, and assessment companies to extend their assessment platforms for mathematics.
Whatever your e-learning product, Algebrakit offers you the tools to handle all math-related challenges.
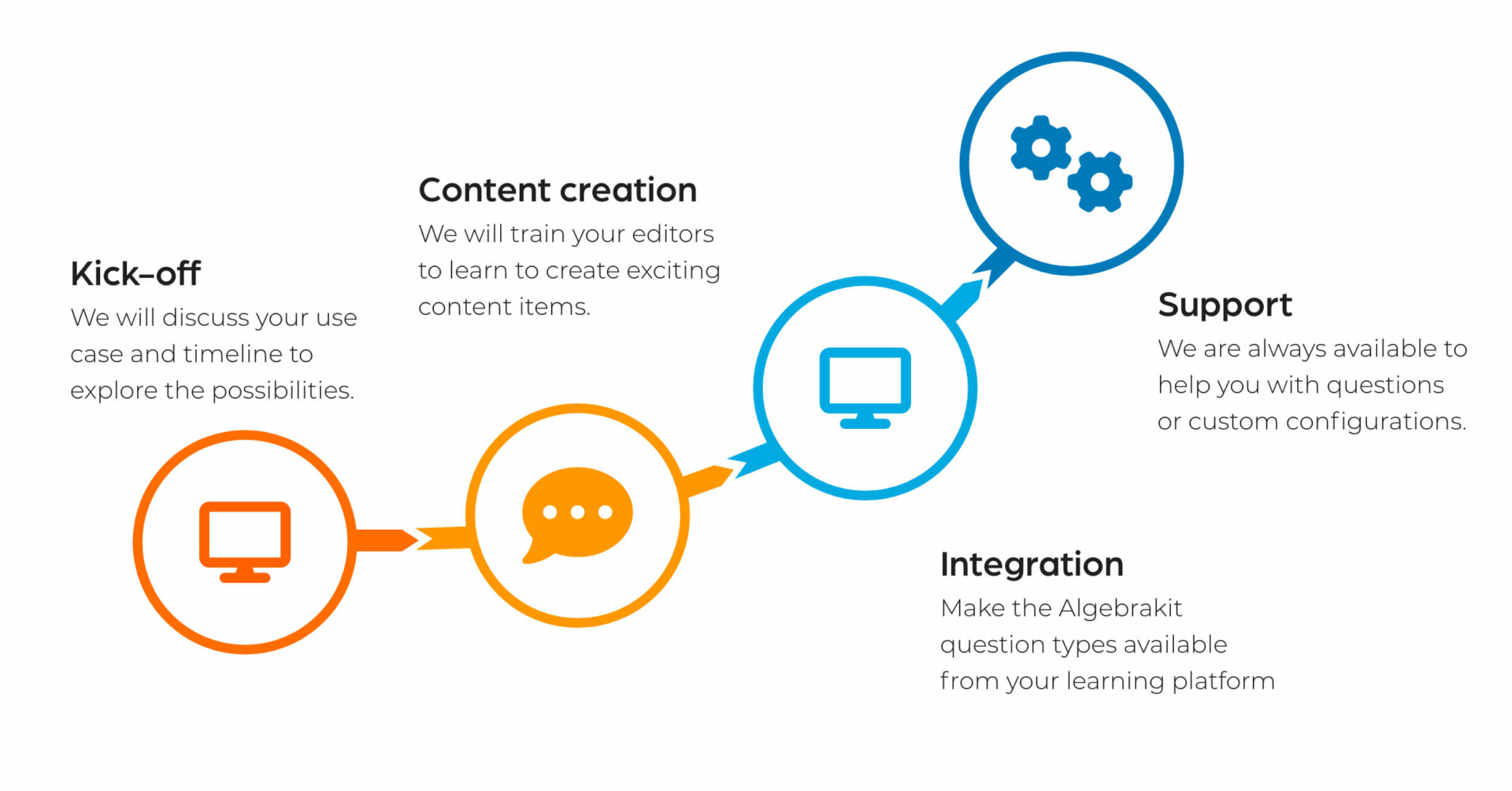
Our proces & services
- Integration services
- Authoring services
- Onboarding services
- Customer support
We support you along the way
We and our ecosystem of partners are available to support you in making the most of Algebrakit.
Content creation
We train and support your authors to create effective and engaging Algebrakit questions. You can find help in our authoring documentation and through our helpdesk.
For bigger migration projects, we have a network of Algebrakit-certified content partners who can help you get the job done.
We realize that every curriculum and publisher has a unique vision of how math should be taught. We work with your content matter experts to configure the Algebrakit system to align with your didactic approach.
Technical integration
Algebrakit is designed to be integrated into existing learning platforms. With the help of our technical documentation and helpdesk, you will be up and running in no time.
Algebrakit is also available through third-party platforms, such as Learnosity and Moodle.
FAQ
Here are some of the questions we often get, along with their answers. Feel free to contact us if you have additional questions!
What school grades are supported?
Algebrakit is designed for multi-step mathematics, which applies mainly to secondary education. Our tools are also used for some multi-step subjects in primary education, such as multi-digit arithmetic and arithmetic word problems.
Does Algebrakit support our curriculum?
The math curriculum differs between countries in many subtle ways. Algebrakit’s math rules are curated to match the requirements for notation, language, and solution strategies. If the curriculum in your region is not yet supported, we can work together to ensure Algebrakit is consistent with your learning resources.
What translations are available?
We currently support English, French, German, Spanish, Portuguese, Lithuanian, and Dutch. We can add other translations upon request.
Does Algebrakit comply with privacy requirements?
Yes. We do not require Personally Identifiable Information (PII) of students. Evaluation results, hints, error feedback, and all other information are stored under a unique session ID. Only you can connect that session ID to the student.