Is EdTech a Stop-Thinking Trap?
It seems like ages ago, but I often think back to my early days as a young math teacher. There was so much to learn— from managing my classroom to finding the best way to introduce a new concept. On my personal journey to becoming a good teacher, often just me and the class, I experienced numerous lows and a few exhilarating highs.
Who’s doing the thinking?
As a math teacher, the spotlight was on activating the student’s thinking process. “Who is doing the thinking here?” was the rhetorical question from my teacher trainer, which echoes in my mind to this day. Are students actively engaged in problem-solving, or are they just passively receiving information?
Good teachers don’t just hand out answers on a silver platter. Instead, they create an environment where students are encouraged to explore, reason, and find solutions working alongside their classmates, their teacher, and sometimes on their own. In this environment, teachers provide strategic nudges that guide students without leading them to the final answer too quickly. This method nurtures critical thinking and fosters a deeper understanding of mathematical principles.
Is EdTech helping?
But what happens when we introduce educational technology (EdTech) into this carefully crafted environment? Most teachers view EdTech as a time-saver, a modern tool that can make their lives easier while appealing to tech-savvy students. It’s true that most students like engaging apps and dynamic platforms. Yet, are these students truly thinking and learning, or are they merely tapping, guessing, and swiping through problems?
AI-powered tools, like ChatGPT and Photomath, provide swift solutions to complex problems, which makes them popular among students. But if students can simply input a problem and receive a ready-made solution, are they genuinely learning?
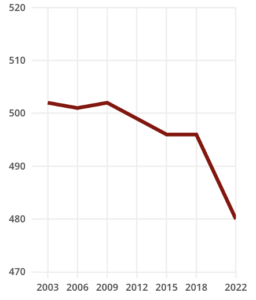
If we look at the numbers, we see little proof that educational technology is helping raise student achievement in math. Test scores among 15-year-olds, according to the international PISA test, have been dropping for the past fifteen years, especially in rich countries. Of course, you cannot just blame EdTech as there can be many reasons for this decline, like increasing immigration (which means more language learners), a higher share of children living in relative poverty, distractions from mobile phones, and an overall reduction in student well-being ([1], [2]). However, despite the fact that spending per student has gone up, there is little evidence that technical innovations have led to a revolution in math learning.
PISA test scores, OECD average
Problem-solving is key
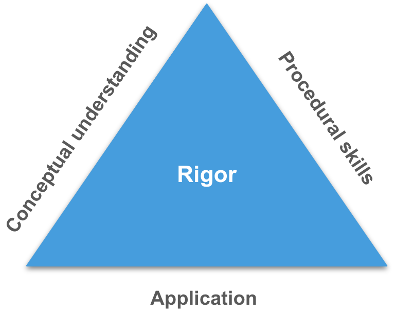
A rigorous understanding of mathematics requires more than just rote memorization of formulas and procedures. It requires a deep conceptual understanding of underlying principles, proficiency in mathematical skills, and the ability to apply this knowledge in various contexts.
For decades, the main approach to developing these three critical components—conceptual understanding, skills, and application—has been through problem-solving.
Problem-solving activities, such as puzzles, riddles, or card tricks, can be very engaging. But when tied to a math curriculum and assessed under time pressure, problem-solving often becomes a source of frustration and anxiety. Students who struggle with math, and sometimes even fear it, often do so because they lack confidence in solving multi-step math problems.
To help students develop a deep understanding of mathematics, we must help them successfully engage with math problems. Peter Liljedahl, a renowned professor of mathematics education, mentions many practices teachers can apply in their classes to improve students’ engagement and ability to solve math problems. His recommendations disrupt the learning environment enough to open the door for student thinking and problem-solving. These practices include students gathering at whiteboards placed vertically around the room, the teacher launching tasks within the first five minutes, and random grouping that changes daily.
Autonomous problem-solving
However, not all learning happens in class. Ultimately, students need to be able to solve problems independently. Without the support of a teacher or their peers, only a minor share of students (31%, according to Liljedahl) have the perseverance to solve problems on their own. The rest find help (if available), cheat, or just don’t do it. This is an opportunity for technology to increase math learning outcomes.
Two principles are essential if we want students to work autonomously on problem-solving tasks:
- Keep the challenge alive: Just as a good teacher knows to refrain from explaining too much too soon, an educational tool should resist the temptation to provide immediate explanations or videos simply because it can. Upholding the challenge is fundamental to promoting deep thinking in problem-solving tasks.
- Keep students engaged. Without teacher guidance and peer support, it is much harder for students to remain focused and resist distractions. Perseverance is crucial, especially for challenging problems where the solution is not immediately apparent. However, perseverance is also a limited resource. Ideally, technology should provide just enough support to keep students engaged without diminishing the challenge.
The Problem-Solving Wishlist
EdTech Wishlist for autonomous problem-solving
Keep the Challenge Alive
| Harmful features | Effective features |
|---|---|
| Giving away answers or intermediate results. | Encouraging students to try something first.
Focusing support on what to try or why something was incorrect. |
| Starting explaining while students are still working on a problem. | Providing short nudges and only when needed to keep students trying. |
| Breaking up a complex problem into smaller parts.
Reducing a thinking activity to a sequence of instructions that does not promote learning. | Presenting the original problem with an empty input area, encouraging to try something first.
Offering multi-layered hints (when needed): |
Keep Students Engaged
| Harmful features | Effective features |
|---|---|
| Evaluating something as incorrect that a human teacher would accept. | Allowing students to skip or combine solution steps.
Accepting equivalent mathematical notations. |
| Focusing on marks. Limiting attempts or time. | Offering a low-anxiety setting where trying is promoted, not punished. |
| Subjecting students to a fixed and inflexible sequence of tasks. | Allowing students to make choices, such as trying a similar or more difficult question.
Presenting problems as an opportunity to check and improve understanding, not an imposed task. |
The Road Ahead
Education is an extensive field, an ecosystem of students, teachers, schools, families, curricula, and now technology. This system has evolved over decades, shaping not only what we know but also how we think and who we are. The core of education is also not technology. We need to design and use tools in a way that fits well with our education system. We don’t need a shortcut but a helpful addition supporting our students in becoming strong, thoughtful problem-solvers.
At Algebrakit, we build math tools to help students master problem-solving. It’s not easy — It has taken us more than a decade working with experts and educators to be where we are today. And we’re always looking to improve.
Because the technology is so complex and the educational ecosystem is so varied, we focused from the start on developing tools that others can use. Today, small and large e-learning platforms, assessment providers, educational publishers, and governments use the Algebrakit API to include problem-solving capabilities in their solutions. Feel free to experiment yourself. Our tutorial and Testbench are excellent free starting points.
Education is one of society’s most important responsibilities. Improving education improves the well-being of every human being. But we have learned that improvement does not come easily, and any claims about “revolutionizing learning” should be met with sincere skepticism. The way up starts with respect for what exists and develops by responsibly exploring the new.