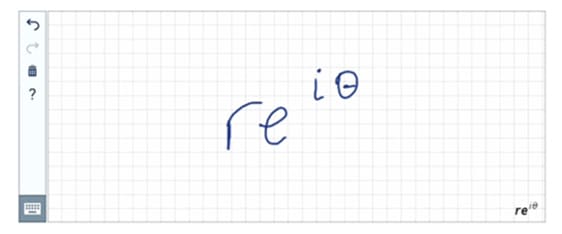On math input methods for online learning
Digital learning offers many benefits for learning mathematics and STEM subjects. From automatic evaluations to unlimited practice and personalized instruction, these tools open up new opportunities to make learning more effective. However, they also present challenges, and one of them is entering mathematical expressions on a digital platform. Math expressions often contain non-standard symbols and use special constructs like fractions, radicals, and exponents. Creating such expressions online can be frustrating and distract students from the math problem they are working on.
Through my experiences at Algebrakit, a specialized provider of digital math learning tools, I have been involved in many discussions about the challenges of math input and possible solutions. The promising news is that several inventive solutions exist for handling math input. However, weighing each option’s strengths and challenges is crucial to finding the right fit.
Approaches to math input
Math input methods mainly center around formula editors and handwriting recognition, such as Optical Character Recognition (OCR) and Stroke-Based Handwriting Recognition.
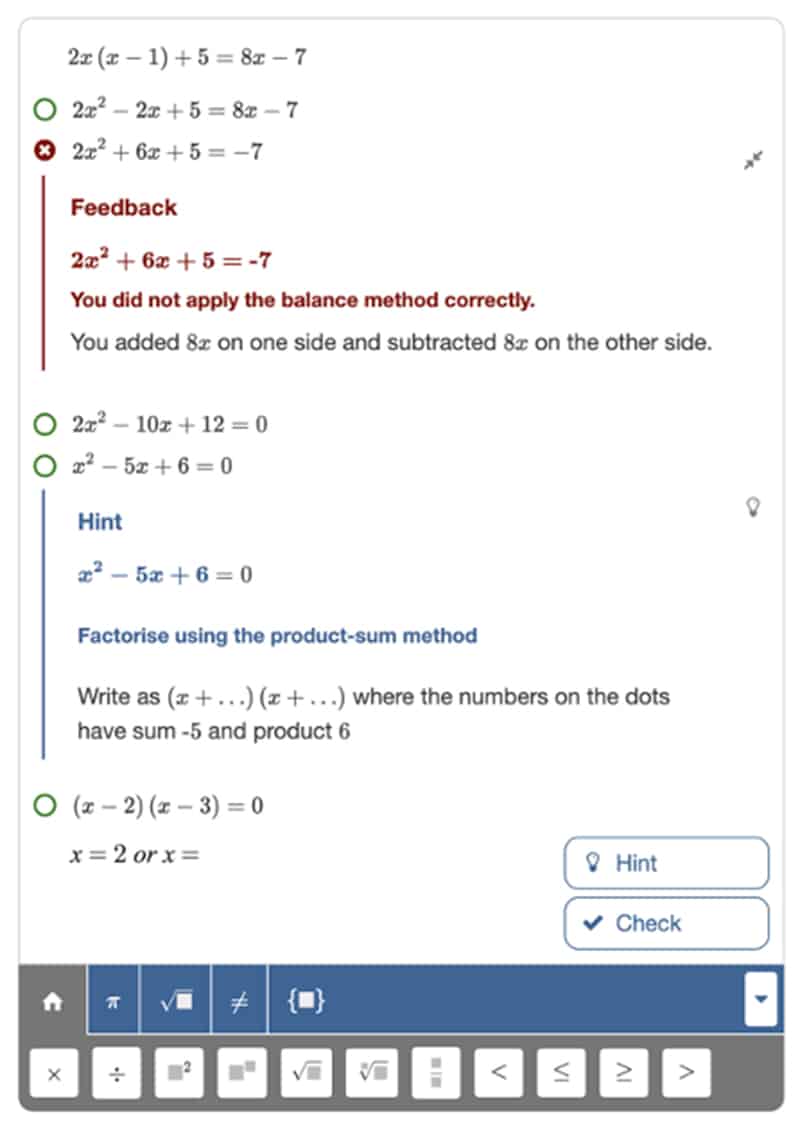
A formula editor is essentially a digital toolbox for math expression creation. It provides buttons for everything students need—fractions, exponents, roots, and symbols. It’s like having a math keyboard that lays out every possible construct.
Figure: Algebrakit’s formula editor
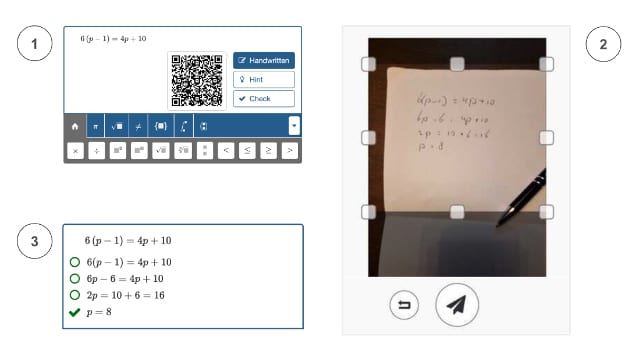
OCR is about extracting text and math expressions from images. Its main advantage is that students can work with pen and paper, avoiding input complexity on a digital device. There are several ways to collect the images. One approach is to let students photograph their work using their smartphones. Alternatively, the print-and-scan method involves preprinted forms where students draft solutions. These forms are collected and scanned, and OCR converts them into digital data. A unique QR code on the form identifies each student’s work, ensuring the work is matched to the right student.
Figure: Using a smartphone to input a worked solution with Algebrakit’s Multistep question type. 1) The student scans a QR code using his smartphone. 2) The smartphone opens the camera app, and the student takes a photo of his work. 3) The student submits the image, and the converted expressions pop up in the learning application, where they are evaluated.
With Stroke-Based Handwriting Recognition (also called Online Handwriting Recognition), students use tablets or smartphones to write directly on the screen. Their input is converted in real-time into neatly typeset math expressions, merging the tactile element of handwriting with the convenience of digital processing.
Figure: The handwriting recognition tool in MathType is an example of Stroke-Based Handwriting Recognition.
Consider: ‘The right tool for the job?’
The right choice of math input solution is a balance between multiple goals. We will introduce these goals first and discuss how they apply to different use cases later.
Convenience
The input method shouldn’t feel like an ordeal but should be both easy to learn and efficient to use. However, ‘easy’ and ‘efficient’ can be conflicting goals. For instance, while formula editors might be simple to learn, constant button presses can become annoying, especially for extensive math expressions. This conflict between easy and efficient can also apply to OCR, as having to take out your smartphone for every math expression poses a lot of overhead, making the whole process inefficient and annoying in the long run.
Device restrictions
Devices vary widely among students—think laptops, tablets, and smartphones. Each needs a compatible method. Online handwriting shines on touch devices, preferably tablets, while OCR is smartphone-friendly. Formula editors can fit anywhere, but their design should complement each device’s screen size and input options. For example, smartphones have limited screen sizes and no physical keyboard, so they must be highly efficient with screen real estate.
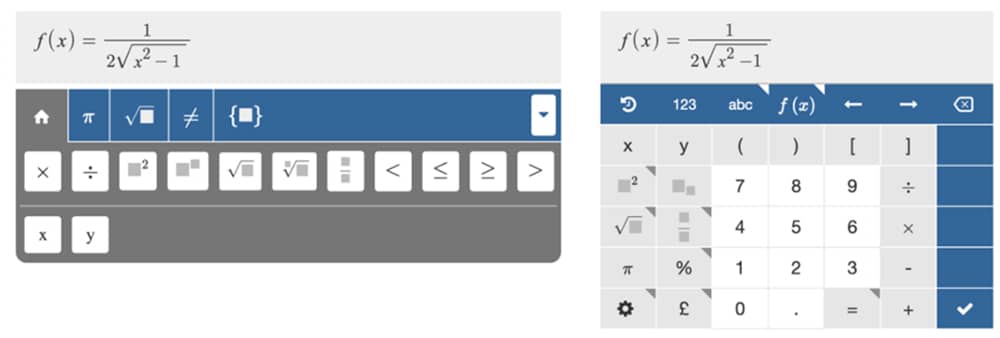
Some argue that students should just use the standard virtual keyboard on tablets and smartphones, as they are already familiar with them. However, such keyboards are optimized for text input and offer the entire alphabet on the main screen. Many math symbols are not available or require switching to a different layout. A good formula editor shows math constructs and symbols on the main screen and restricts letters to those applicable to the math problem.
Figure: the virtual keyboard on smartphones and tablets is not optimized for math expressions.
Reliability
Handwritten math can sometimes play tricks, turning a ‘9’ into a ‘g’ or a ‘0’ into an ‘O’. The risk of misinterpretation is high with OCR if these subtleties aren’t managed correctly.
Typical OCR mistakes |
| Mixing up
– ‘1’, ‘i’ or ‘(‘ – ‘6’ or ‘b’ – ‘5’ or ‘s’ – ‘O’ vs ‘0’ (zero) or (degree) |
| Interpreting ‘)(‘ (two brackets) as ‘x’ |
| Not handling strike-through text correctly. |
You can curb such slip-ups by allowing students to double-check and amend their inputs before submitting. However, this imposes extra overhead and reduces input efficiency. For print-to-scan solutions, it is the teacher who has to double-check the OCR.
Accessibility
Universal access to education means catering to students with a range of needs, such as those with limited eyesight or physical limitations. These students must be able to perceive, understand, and operate the formula editor. Some students use assistive technology, such as text-to-speech or alternate keyboards, which must interact seamlessly with the formula editor.
You can find the many requirements for accessibility in the WCAG standard; addressing those is a lot of work. We spent months understanding the requirements, refactoring the existing code, adding new features, and auditing our new formula editor for WCAG compliance. However, addressing accessibility is no longer optional. It is a global necessity and a legal compliance restriction in many regions, including the US and the European Union.
Cost
Solutions to complex technical problems come at a cost. These costs typically fall under one of the three pricing models:
- Custom Development: You can develop your own solution by paying engineers to build and maintain it. This can be sensible if your use case does not require advanced math input. However, if you need to support secondary or higher education, support mobile and desktop devices, and be WCAG compliant, you’re better off licensing an existing solution.
- SaaS API—Request-Based: Many API providers offer services for which you pay per use. The OCR service MathPix, for example, costs around 2.50 US dollars per thousand requests.
- SaaS API—User-Based: Other suppliers, like Algebrakit, charge per user, regardless of the number of requests. The advantage of such models is that costs are known beforehand and typically half a dollar or less per student per year when acquired at scale.
Use cases
Depending on your use case, some goals are more important than others. Let’s consider a few of these use cases here.
Formative assessment in learning applications
Formative assessment is done while students are learning. The results from the exercises are not intended for grading but to provide feedback to students and teachers so they can correct misconceptions and monitor learning progress. Immediate feedback is crucial here because you want students to receive the feedback while the math problem is still in working memory. Therefore, the input method should exclude any extra steps or wait times.
Summative assessment
A summative assessment tests for understanding after the learning phase. Evaluating student input does not have to be immediate, as students will not receive feedback from the system during the assessment. This is why some assessment platforms support Print & Scan solutions, where students work offline, writing on paper forms scanned and converted through OCR after the assessment. A drawback of Print & Scan is that the forms must be collected and processed, requiring students to take the assessment at school.
Summative tests generally involve time constraints and an increased level of anxiety. More so than for formative assessment, inputting math expressions must be convenient and straightforward. If a formula editor is used, make sure students have been able to practice with the question types so they don’t have to spend time and attention investigating how to type an expression. Here is a short example of how we onboard students to the Algebrakit formula editor.
Math and text integration
Some subjects require students to weave mathematical reasoning seamlessly with textual explanation. Rapid toggling between text and math is invaluable. An inline editor activated by a simple keyboard command could save time and frustration.
Figure: Algebrakit editor for text and mathematics. Pressing the space bar twice brings up the math editor. Try it online.
Figure: Algebrakit editor for text and mathematics. Pressing the space bar twice brings up the math editor. Try it online.
Multi-step problem-solving
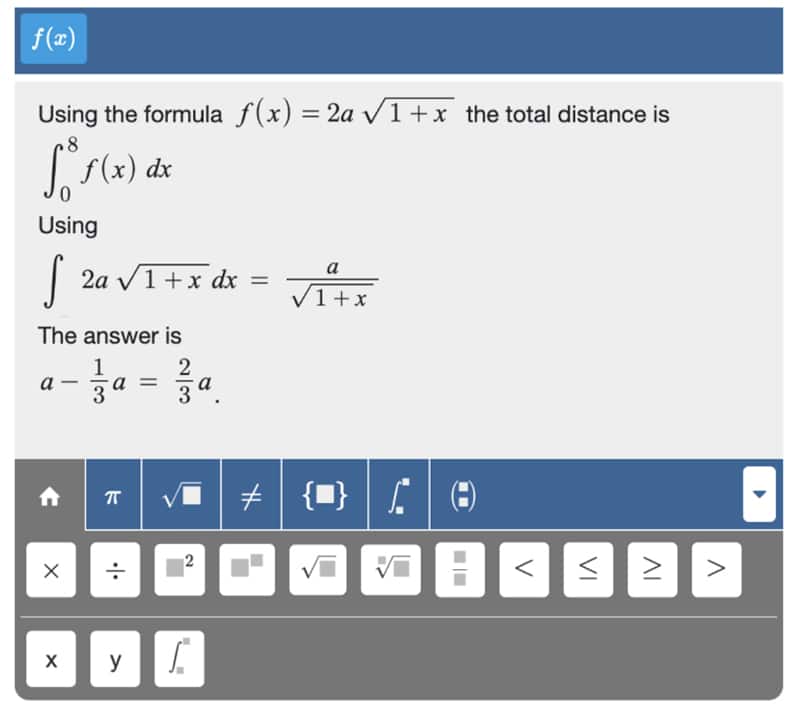
Problem-solving is core to learning mathematics. For multi-step problems, students input multiple expressions to answer a single question, where every expression is often a rewrite of the previous one. In such cases, it is even more critical that entering math expressions can be done efficiently.
At Algebrakit, we use a range of innovative features, such as the ability to recall and update the previous expression, offering the most relevant buttons on a quick-launch bar, and using efficient shortcuts to allow working with the keyboard. With some practice, entering math expressions with the Algebrakit formula editor is faster than pen and paper.
Summary
Here is a short overview of the use cases, considerations, and options we discussed:
| Use case | Considerations | Suitable options |
|---|---|---|
| Tutoring applications | Focus on efficiency Process input instantly to enable immediate feedback. |
1. Formula editor 2. Stroke-based Handwriting Recognition (touch devices only) |
| Summative assessment | Focus on ease of use and reliability | 1. Formula editor 2. Print & Scan 3. Stroke-based Handwriting (touch devices only) |
| Math in text | Focus on the integration of formulas in the text. | 1. Embedded formula editor 2. Full-page OCR |
| Multi-step problem-solving | Focus on efficiency. | 1. Formula editor 2. Stroke-based Handwriting Recognition (touch devices only) 3. Print & Scan (but no feedback) |
Final thoughts
Math expression input is just one of the many technical challenges of online math learning. Other requirements include automatically evaluating answers, providing feedback on intermediate steps, and offering question types that support the full range of math activities.
At Algebrakit, we made it our core business to solve such difficulties and bring our tools to learning providers. Feel free to try some demos on our website or read our tutorial to understand what is possible.